Фильтр Калмана: простыми словами о сложной математике
Если вы занимаетесь разработкой роботов или автопилотов, то вы наверняка уже слышали о Фильтре Калмана. Но что это такое и как он работает?
Обычно, при знакомстве c Фильтром Калмана, обывателя встречает множество сложных формул. В данной статье мы объясним эти математические понятия простыми словами на конкретных примерах.
Рисунок 1 – Непонятные формулы
Что такое Фильтр Калмана?
Фильтр Калмана — это математический алгоритм, который позволяет оценивать состояние системы на основе неполной, зашумленной информации. Это может быть любая система, которую нужно контролировать или управлять (робот, дрон, автомобиль или процесс в производственной линии).
Фильтр Калмана был разработан Рудольфом Калманом в 1960 году и стал широко использоваться во многих областях, включая авиацию, автомобильную промышленность, медицину и даже бытовую технику. Он позволяет получать более точную оценку состояния системы, чем простое считывание данных с сенсоров.
Рисунок 2 – Рудольф Калман
Как работает Фильтр Калмана?
Фильтр Калмана работает на основе принципа прогнозирования и корректировки. Сначала он прогнозирует будущее состояние системы на основе текущего состояния и информации о ее движении. Затем он корректирует этот прогноз на основе новой информации от сенсоров.
Каким образом происходит прогнозирование будущего или осознание текущего состояния системы? Для начала разберем необходимую терминологии из теории вероятностей.
1. Немного из теории вероятности:
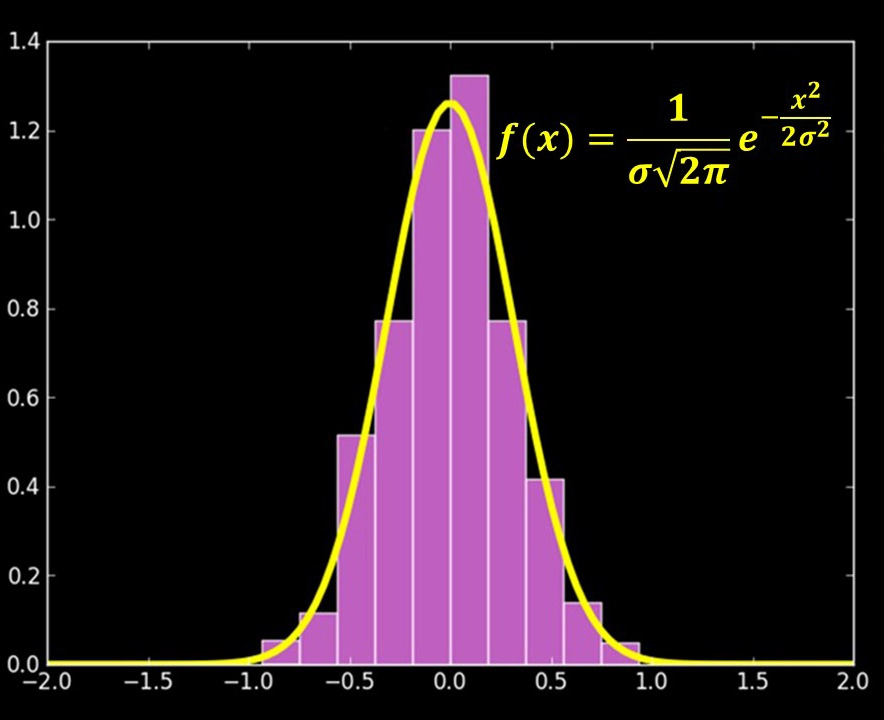
Если много раз измерять какую-то величину, то получится множество точек, разбросанных вокруг этой величины. Такие измерения, в большинстве случаев, описываются нормальным законом распределения, а функция, которая их описывает называется кривой Гаусса (Гауссианом).
На рисунке показан нормальный закон распределения случайной величины X в виде гистограммы. Горизонтальная ось показывает измеренное значение, а вертикальная – количество измерений, попавших в интервал и нормированное по высоте таким образом, чтобы площадь под графиком была равна единице.
Рисунок 3 – Пример нормального закона распределения
Это делается для того, чтобы кривая Гауссиана представляла собой функцию распределения вероятностей.
У гауссиана есть два основных параметра:
– математическое ожидание (середина графика, на рисунке 3 – это ноль)
– среднеквадратическое отклонение (сигма, σ).
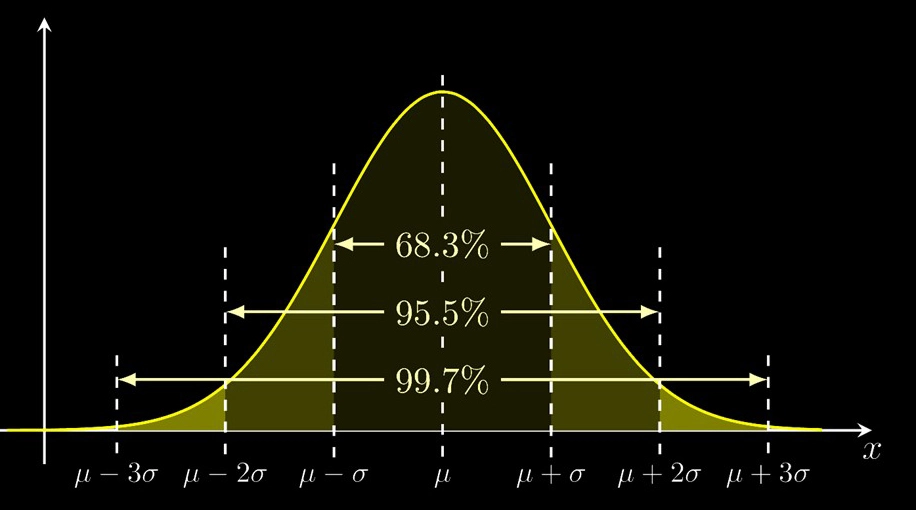
В зависимости от математического ожидания и сигмы гауссианы имеют разную форму и “центр” (рисунок 4).
Чем меньше сигма, тем выше и тоньше гауссиан. При этом площадь под гауссианом, описывающим распределение величины, всегда одинакова и равна единице.
Рисунок 4 – Форма гауссианы в зависимости от её параметров
Как параметр среднеквадратическое отклонение (сигма, σ) соотносится с гауссианом?
Для любого гауссиана отрезок ±σ содержит 68,3% площади под графиком, для интервала ±3σ это значение уже 99,7%. Это означает, что 99,7% всех измерений лежит в промежутке от минус трёх до трёх сигм.
Рисунок 5 – Количество измерений, попадающих в разные интервалы
2. Пример с роботом-пылесосом
Давайте рассмотрим конкретный пример, чтобы лучше понять, как это работает.
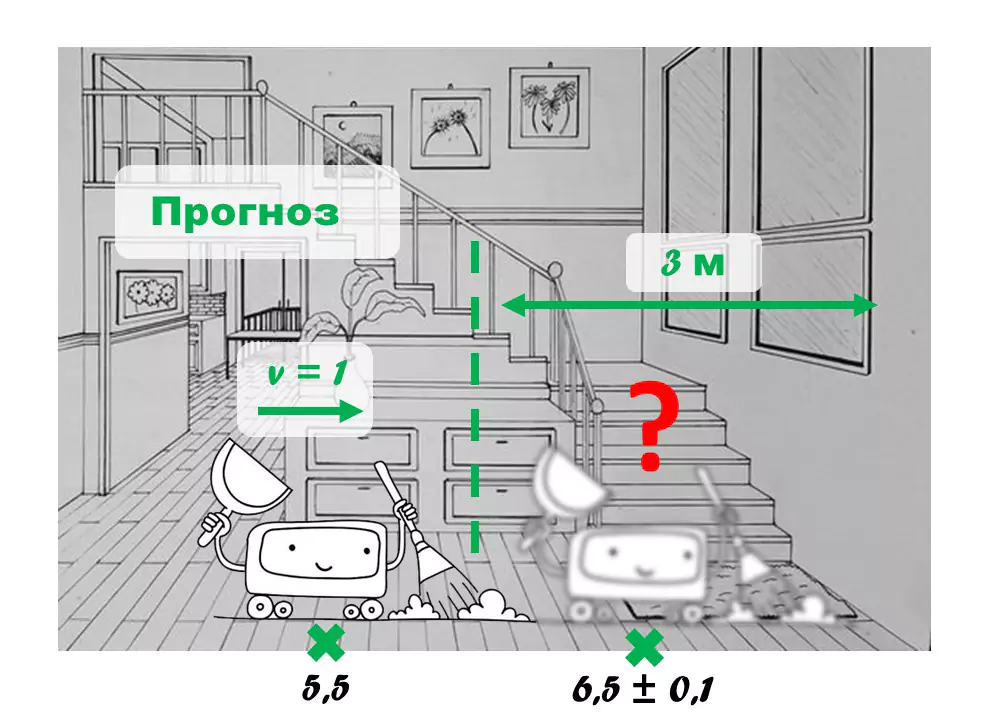
Предположим, у нас есть робот-пылесос, который перемещается по комнате и собирает пыль. Он оснащен сенсорами, которые позволяют ему определять свое положение в пространстве и расстояние до объектов (стен, мебели). Однако из-за шума и неточности в сенсорных данных мы не можем точно определить местоположение робота.
Фильтр Калмана решает эту проблему, как мы разобрали выше, через прогноз и коррекцию.
1) Алгоритм прогнозирует новое местоположение робота, основываясь на предыдущей информации о его положении и скорости движения. Например, если робот находился в точке (5, 5) и двигался вправо со скоростью (1, 0), то следующая позиция должна быть (6, 5). Но из-за неравномерности движения, помех на пути и шумов в датчиках мы не можем быть полностью уверены в этом. Поэтому фильтр также оценивает ошибку своего прогноза. Пусть в данном случае наш прогноз будет (6, 5) по координатам с отклонением σ = 0.1 метров.
Рисунок 6 – Прогноз нового местоположения
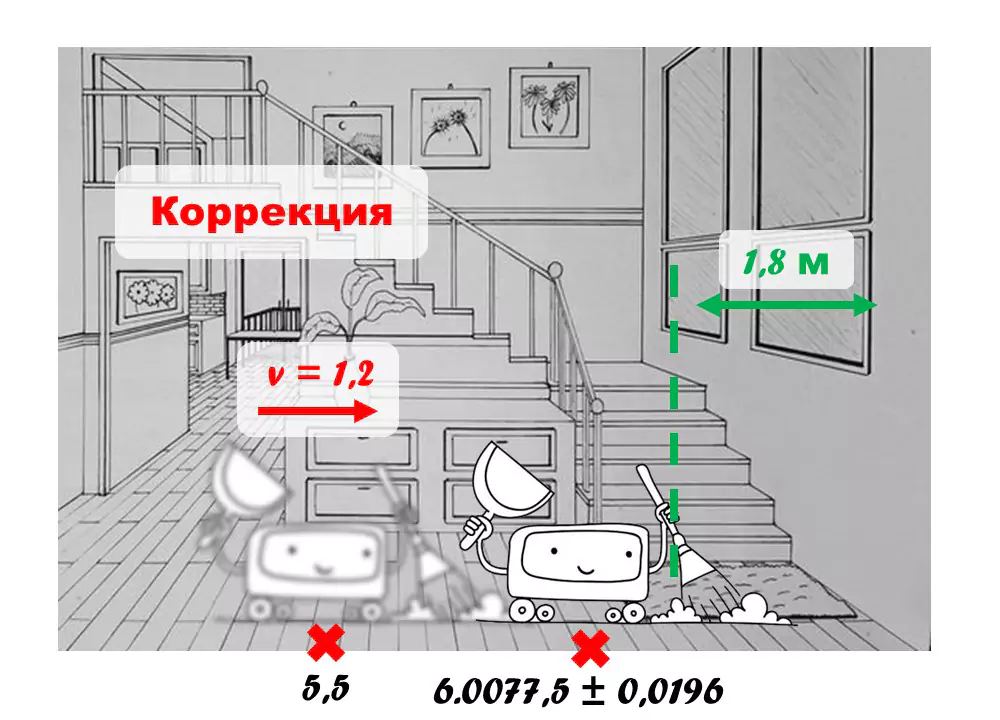
2) Алгоритм корректирует прогноз на основе новой информации от сенсоров. Например, датчики робота сообщили, что расстояние до стены сейчас равно 1,8 метра, тогда как на прошлом временном шаге расстояние до стены было 3 метра. Это означает, что робот за это время проехал не 1, а 1.2 метра. Датчик расстояния имеет хорошую точность, около нескольких сантиметров (σ = 0,02 м), поэтому при корректировке фильтр Калмана будет больше полагаться на данные датчика расстояния.
Рисунок 7 – Коррекция прогноза местоположения
В данном случае, Фильтр Калмана предскажет, что робот в новом положении будет иметь координаты (6.0077,5) с обновленным отклонением σ = 0,0196 м.
Фильтр Калмана: формулы и математика
Простыми словами, Фильтр Калмана позволяет определить оптимальную оценку состояния системы, учитывая имеющуюся информацию и шум. Фильтр Калмана является математическим алгоритмом, и он использует формулы для вычисления оптимальной оценки состояния системы.
Фильтр Калмана использует два типа формул:
1) Формула прогнозирования будущего состояния системы, основываясь на предыдущей информации о ее состоянии и движении:
2) Формула корректировки прогноза, основываясь на новой информации от сенсоров:
Еще один пример
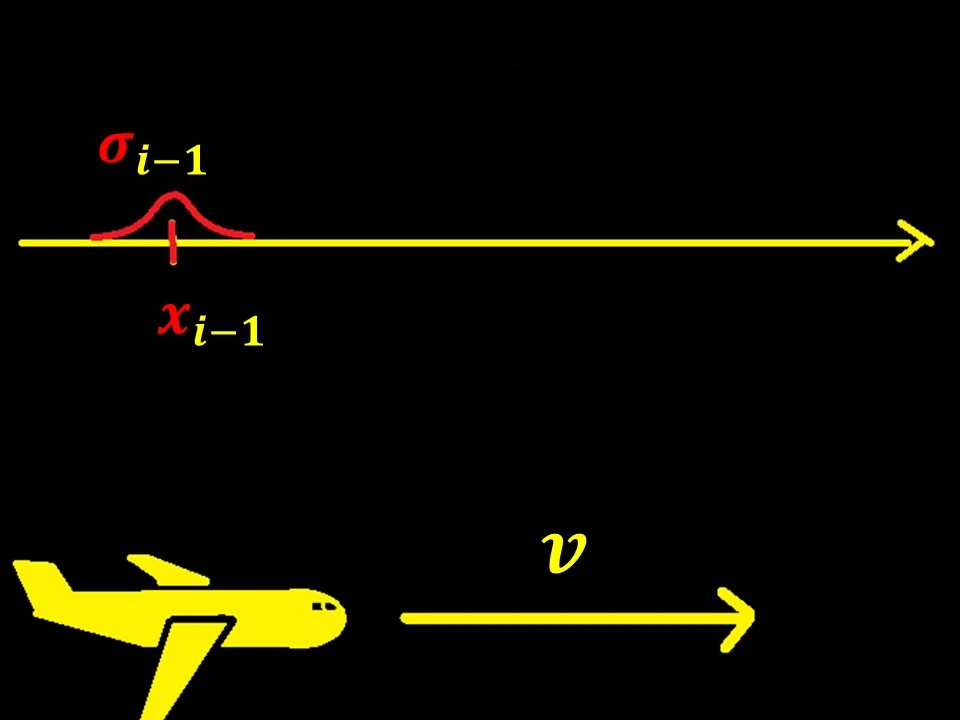
Разберем принцип работы Фильтра Калмана на примере одномерного полёта самолёта.
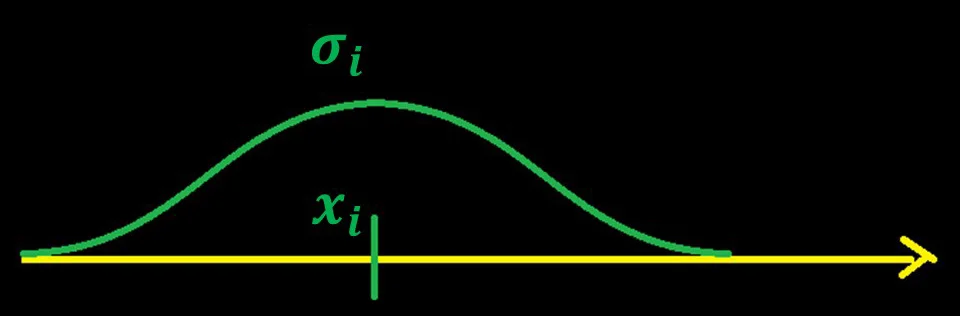
Самолёт летит вправо вдоль оси x со скоростью v. Допустим, мы знаем его координату в предыдущий момент времени
xi-1 c погрешностью (сигмой) σi-1.
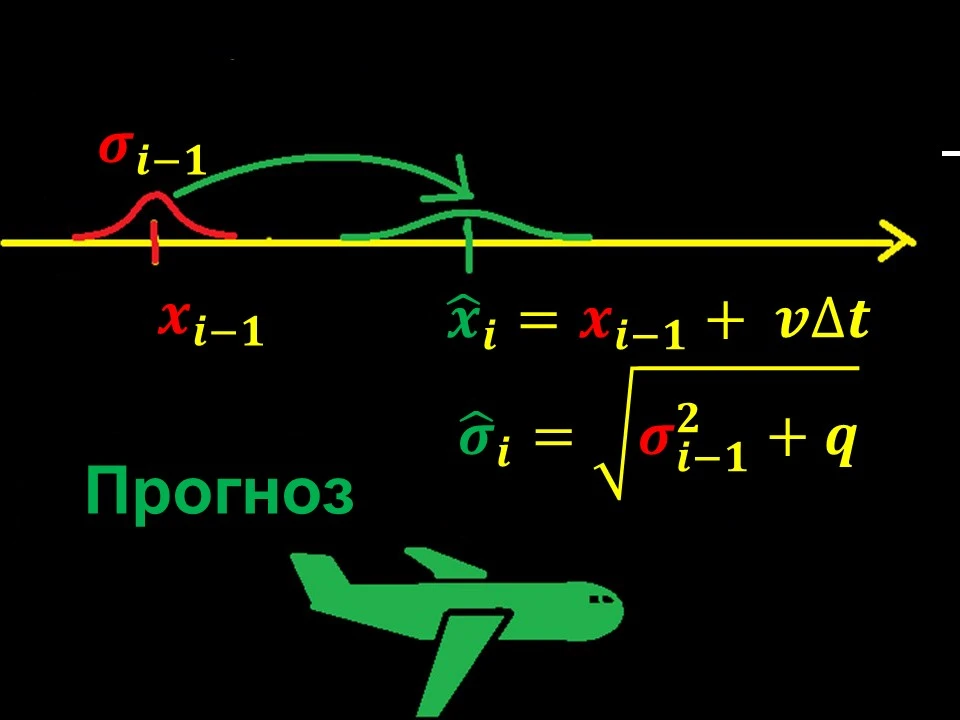
Для вычисления координат в текущий момент времени сначала исполняется шаг предсказания.
Рисунок 8 – Полет одномерного самолета
По известной кинематической модели (в данном случае это прямолинейное равномерное движение) вычисляется предсказание координаты ͡xi и предсказание ошибки определения этой координаты ͡σi по прошлым данным.
Прогноз ошибки получается путем искусственного добавления погрешности q на каждой итерации.
В тех случаях, когда по тем или иным причинам не происходит шага коррекции, шаг прогноза должен постоянно увеличивать ошибку определения состояния из-за погрешностей модели, нелинейности движения и вычислительных погрешностей.
Рисунок 9 – Предсказание положения самолета
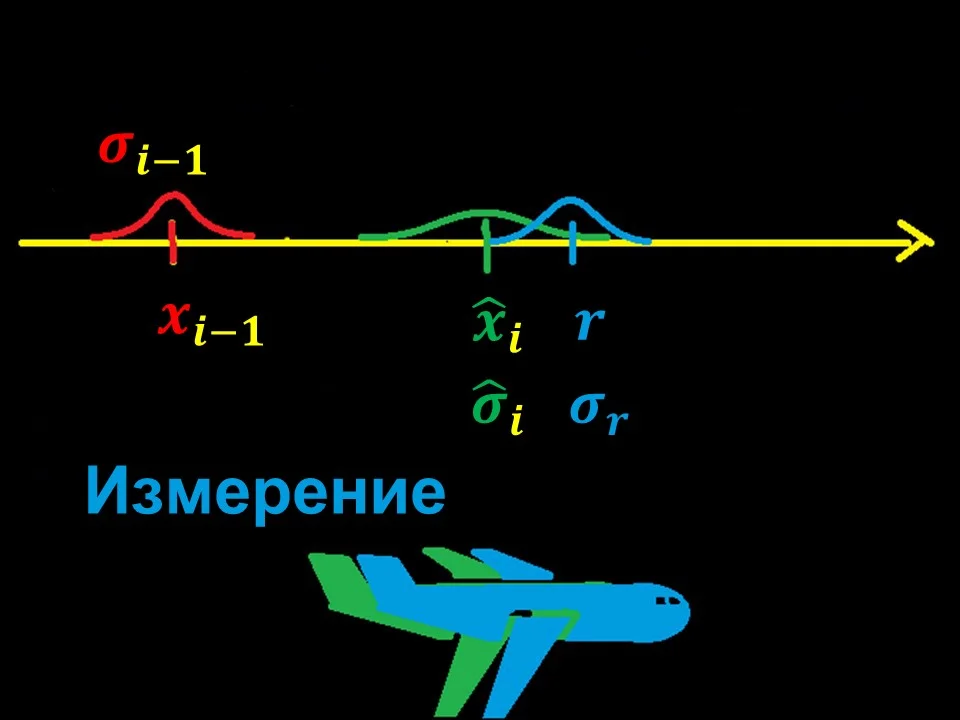
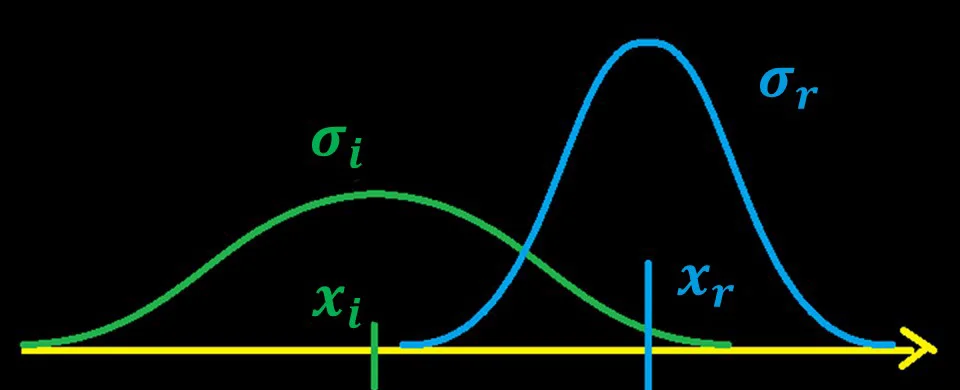
Помимо предсказания на каждой итерации нам также известны измеренные координаты самолёта r.
Это можно сделать, например, при помощи GPS приёмника. Однако само измерение координаты r неточно и имеет свою погрешность σr.
Рисунок 10 – Измеренные координаты самолета
Итоговый шаг – коррекция.
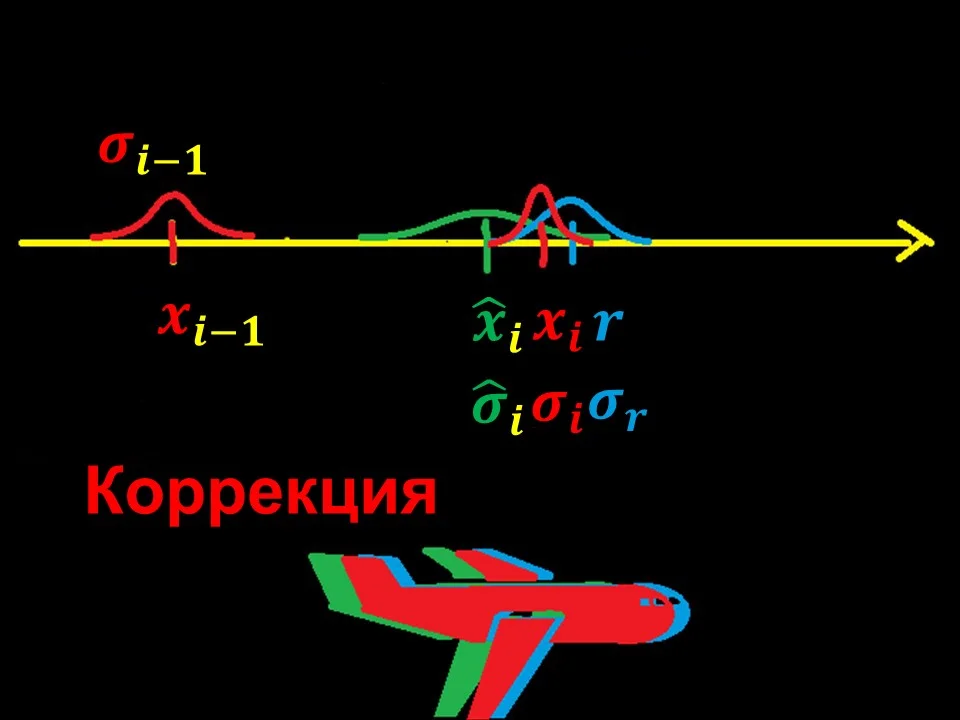
На этом шаге предсказанная ранее координата ͡xi уточняется измерением r. Чем точнее мы знаем нашу измеренную координату r (т.е. чем меньше сигма σr) тем ближе итоговая координата xi будет к измерению r. И наоборот, чем хуже точность GPS приемника, тем больше мы будем полагаться на предсказанную координату ͡xi
Рисунок 11 – Коррекция положения самолета
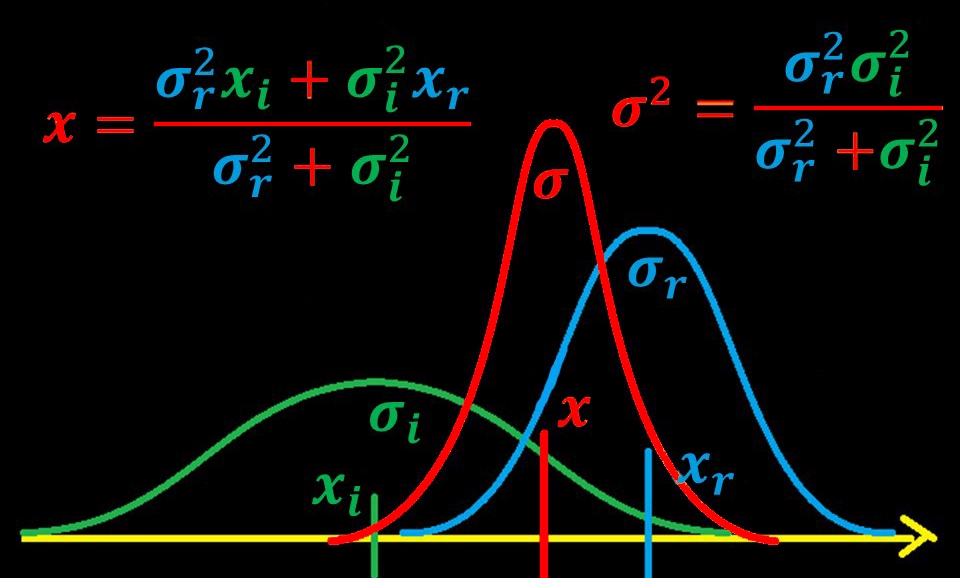
Непосредственно за вычисление итоговой координаты отвечает коэффициент К, так называемое ядро фильтра Калмана.
Если K близко или равно нулю, то итоговая координата xi будет близка к предсказанному значению ͡xi. Если K близок к единице, то итоговое значение xi будет ближе к измерению r.
Рисунок 12 – Вычисление итоговой координаты
Рассмотрим подробнее умножение двух гауссиан на этапе коррекции.
Предположим, что оценка ошибки положения велика (сигма относительно большая, график “широкий и приплюснутый”).
Рисунок 13 – Оценки ошибки положения
А оценка погрешности измерений наоборот более маленькая (сигма меньше, график выше и “уже”).
Напоминаем, что площадь под каждым графиком одинакова и равна единице.
Рисунок 14 – Оценки ошибки положения и погрешности измерений
Тогда результат “нормализованного умножения” (перемножение двух гауссиан с последующим масштабированием графика до единичной площади под ним) двух гауссиан будет таким, как показано на рисунке 15.
При этом результат коррекции находится ближе к измерению xr, что обусловлено меньшей сигмой σr. Результирующая сигма будет меньше чем любая из исходных.
Рисунок 15 – Нормализованное умножение гауссиан
Теперь при встрече с фильтром Калмана и его “страшными” формулами у пользователя остается меньше вопросов.
Рисунок 16 – Не такие уж и непонятные формулы
Заключение
Фильтр Калмана – это мощный алгоритм, который используется в различных областях, включая робототехнику, автомобильную промышленность, аэрокосмическую инженерию и другие. Он позволяет определять оптимальную оценку состояния системы, учитывая шум в данных от сенсоров и предыдущую информацию о состоянии системы.
Хотя математика Фильтра Калмана может показаться сложной, его концепция может быть объяснена в простых словах. Важно помнить, что Фильтр Калмана – это инструмент, который может помочь в обработке данных и улучшении точности прогнозирования в различных приложениях.
Подписывайтесь на наш Telegram канал: https://t.me/mplab
На этом канале мы публикуем: кейсы (наши статьи и исследования); информацию о продуктах (модификации и новинки); отвечаем на часто задаваемые вопросы и другие анонсы.
